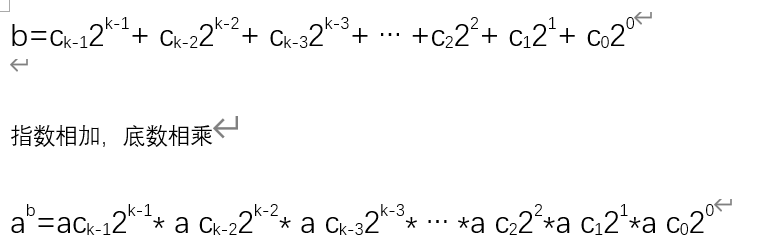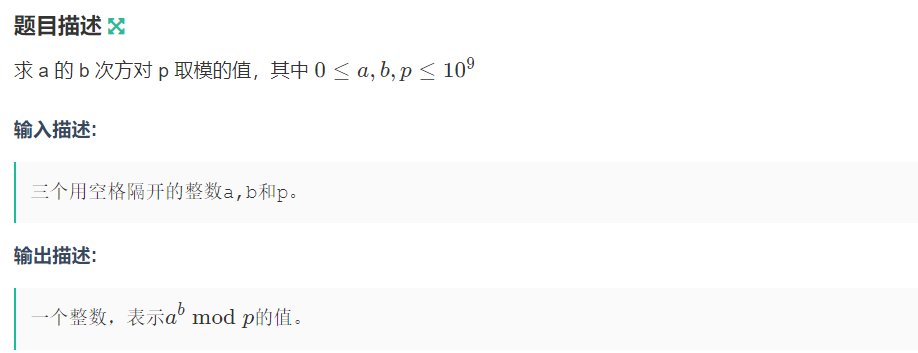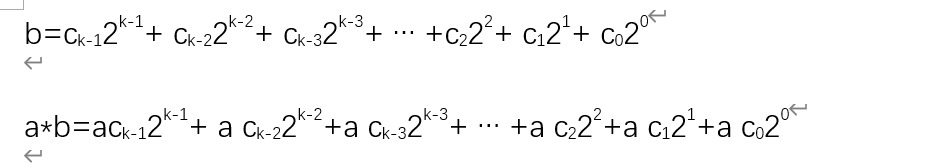前言

暑假在看c++面经时，看到了腾讯的一道面试题。

题目大意是：求(2^1e10)%10000的值，限制了时间复杂度。

在C++中没有Java和Python中的大数，不知道读者朋友们可否AC此题。

正文

这道题可以用快速幂来AC。
请听我详细道来。

在学习了二进制相关知识后，我们知道任何一个数都可以用唯一的二进制表示，也就是说每一个数可以唯一表示为若干指数不重复的2的次幂的和。

举个例子：假设b在二进制表示下有k位。则b可以表示为：

b=ck-12^k-1^+ck-22^k-2^+ck-32^k-3^+……+c12^1^+c02^0^

快速幂常见的模式为：

1. 给定a,b,p的值，求(a^b)%p的值。a,b,p都是大数，1<= a ,b ,p<=1e10.
2. 给定a,b,p的值，求(a*b)%p的值。a,b,p都是大数，1<= a ,b ,p<=1e10.

1. (a^b)%p

有上面的例子可知：

b=ck-12^k-1^+ck-22^k-2^+ck-32^k-3^+……+c12^1^+c02^0^

则 a^b= a^ck-12k-1^+a^ck-22k-2^+a^ck-32k-3^+……+a^c121^+a^c020^

由于数学格式支持的不是很好，贴一个图说明一下。

算法分析：

根据上式我们发现，原问题被我们转化成了形式相同的子问题的乘积，并且我们可以在常数时间内从2^k-1^项推出 2^k^项。

这个算法的复杂度是O(logN) 的，我们计算了logN个 2^K^次幂的数，然后花费 logN 的时间选择二进制为 1 对应的幂来相乘。

来个题目练练手 ：计算 (a^b)%p的值

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

#include<iostream>

using namespace std;
typedef long long LL;
LL a,b,p;

int main()
{
    scanf("%lld%lld%lld",&a,&b,&p);
    LL ans=1%p;        // 初始ans
    while(b)
    {
        if(b&1) ans=ans*a%p;
        a=a*a%p;       //反复平方
        
        b>>=1;
    }
    printf("%lld\n",ans);
    return 0;
}

2.(a*b)%p

同第一张模板类似，同理：

来道题练练手：求(a*b)%p

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

#include<iostream>
using namespace std;

typedef long long LL;
LL a,b,p;
LL ans;

int main()
{
    scanf("%lld%lld%lld",&a,&b,&p);
    while(b)
    {
        if(b&1) ans=(ans+a)%p;   // 累加每个2^k
        a=a*2%p;   
        b>>=1;
    }
    printf("%lld\n",ans);
    return 0;
}

注意事项

由于快速幂的数据很大，在使用c++做题时，用单纯的cin来输入测试用例很慢，会导致超时。

在这里给两个小建议：

1. cin前面加上这条取消同步的语句

1

cin.tie(nullptr)->sync_with_stdio(false);

2. 用scanf()来读取。

最后

关于快速幂的题型还有很多，比如快速幂矩阵，计算斐波那契数等。

这篇文章所讲的只是快速幂的初阶内容，我在后面会为大家分享更高阶的快速幂知识。

好啦，就先到这里了。我们下期再见！

前言

学习Linux系统已有一段时间，今天分享一些linux基础指令。

基础指令（1）涉及的指令有ls,pwd,cd,touch,mkdir,rm指令。

正文

1 .ls 指令

ls是 list 的缩写。

语法格式: ls [选项] [文件]
默认状态下，ls命令会列出当前目录的内容。而带上参数后，我们可以用ls做更多的事情。

• -a 列出目录下的所有文件，包括以 . 开头的隐含文件。

• -d 将目录象文件一样显示，而不是显示其下的文件。 如：ls –d 指定目录

• -i 输出文件的 i 节点的索引信息。 如 ls –ai 指定文件

• -k 以 k 字节的形式表示文件的大小。ls –alk 指定文件

• -l 列出文件的详细信息。

• -n 用数字的 UID,GID 代替名称。 （介绍 UID， GID）

• -F 在每个文件名后附上一个字符以说明该文件的类型，“*”表示可执行的普通文件；“/”表示目录；“@”表示符号链接；“|”表示FIFOs；“=”表示套接字(sockets)。（目录类型识别）

• -r 对目录反向排序。

• -t 以时间排序。

• -s 在l文件名后输出该文件的大小。（大小排序，如何找到目录下最大的文件）

• -R 列出所有子目录下的文件。(递归)

• -1 一行只输出一个文件。

演示实例：

解释一下.和..

在上面的演示实例中，我们看到了.和. .。

.表示当前目录

.. 表示上级目录。

2. pwd命令——显示当前路径

功能：显示用户当前所在的目录

演示：

3. cd 指令

功能：改变工作目录。将当前工作目录改变到指定的目录下。

• cd .. : 返回上级目录
• cd /home/litao/linux/ : 绝对路径
• cd ../day02/ : 相对路径
• cd ~：进入用户家目
• cd -：返回最近访问目录

4. touch指令

功能：touch命令参数可更改文档或目录的日期时间，包括存取时间和更改时间，或者新建一个不存在的文件。

• -a   或–time=atime或–time=access或–time=use只更改存取时间。
• -c   或–no-create 不建立任何文档。
• -d 使用指定的日期时间，而非现在的时间。
• -f 此参数将忽略不予处理，仅负责解决BSD版本touch指令的兼容性问题。
• -m   或–time=mtime或–time=modify 只更改变动时间。
• -r 把指定文档或目录的日期时间，统统设成和参考文档或目录的日期时间相同。
• -t 使用指定的日期时间，而非现在的时间。

5. mkdir指令

语法：mkdir [选项] dirname
功能：在当前目录下创建一个名为 “dirname”的目录

• -p 递归创建多级目录
• -m 建立目录的同时设置目录的权限

mkdir –p test/test1 : 递归建立多个目录

6. rmdir指令 && rm 指令

rmdir是一个与mkdir相对应的命令。mkdir是建立目录，而rmdir是删除命令。

rm命令可以同时删除文件或目录

语法：rm [-f -i-r-v] [dirName/dir]

适用对象：所有使用者

功能：删除文件或目录

常用选项：

• -f 即使文件属性为只读(即写保护)，亦直接删除
• -i 删除前逐一询问确认
• -r 删除目录及其下所有文件

演示：

ps: 删库跑路
学到rm指令，我们会下意识是想到删库跑路的梗。

rm也是一个危险的命令，使用的时候要特别当心，（比如在/（根目录）下执行rm * -rf）。。。。后果很严重。

所以，我们在执行rm之前最好先确认一下在哪个目录，到底要删除什么东西，操作时保持高度清醒的头脑。

结语

Linux的指令数不胜数，初学者要抓住linux的重要常见指令，敲烂键盘，记住指令。

下一次继续分享基础重要指令（2），咱们一起学指令，下一篇见。

博客园文章：https://www.cnblogs.com/bat1024996/p/15221167.html

大家好，我是希达。

前言

最近学习了算法导论上的快速排序部分，有不少体会。

今天就来分享一下。在此欢迎大家批评指正文中的错误。

快速排序

正文

1.快速排序的优点

说起快速排序，它的名字就显现出快排最大的优点————快。到底有多快呢？咱们用数据说话:

综合一般情况来说，快排确实有(亿点快)。特别是对较大数据量的排序。

快速排序的综合时间复杂度是O(nlgn),但在极端最坏情况下，时间复杂度会到O(n^2)。

很多人在看到O(n^2)会产生疑问？为什么我们还要在实际生活中使用快排呢。

尽管快排的最坏时间复杂度很差，但是它的平均性能好，通常是实际排序中最好的选择。它的期望时间复杂度是O(nlgn)，(绝大多数是这样，在下文快排的性能分析中会有说明)，在排序中很少遇到最坏情况。并且O(nlgn)中隐含的常数因子非常小。
在C++库函数中sort()函数底层大部分用快排实现的(可以参照下文的小区间优化)。

所以：快排，yyds！！！

2.快排的原理及实现

我们来理解快排的原理。快排运用了分治的思想。

在每一次排序中，选取一个数据作为主元x，在将数据的每个值与主元x进行比较，使每趟排序结束时，小于或等于x的在x数据的左边，大于或等于x的在x的右边。(和x相等的数可以在x的两侧，这就造成了快排的不稳定性)。

左子区间都是不大于x的数，右子区间都是不小于x的数。以x为界限，递归左右子区间。从大致有序到全部有序。

下面我们来简单实现快速排序。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

void quick_sort(int *a, int l, int r)
{
	if (l >= r)
		return;
	int x = a[l];    // 取最左边的值作为主元x
	int i = l, j = r;
	while (i < j)
	{
		while (a[i] <= x && i<r) ++i;    // 循环结束时a[i]比x大
		while (a[j] >= x && j>l) --j;    // 循环结束时a[j]比x小
		if (i < j)
			swap(a[i], a[j]);       // 交换a[i],a[j]
	}
	// j为分界点
	swap(a[l], a[j]);     // 将主元x放在正确的位置，作为分界点

	// 递归左右子区间
	quick_sort(a, l, j - 1);
	quick_sort(a, j+1, r);
}

3.快排的性能分析

我们对上面的代码进行分析：

1. 最理想的情况：每次循环的主元x都在区间的中间，遍历一次数据的复杂度为O(n)，递归次数为lgn，所以时间复杂度为O(nlgn)。

2. 最坏的情况：当输入的数据基本有序(逆序)时，在递归时，产生两个大小为n-1和0的子区间，使递归的深度为n，时间复杂度变为O(n^2)。效率不及插入排序（后面会介绍用插入排序实现小区间优化以减少递归的栈深度）

3. 就平均情况来看。左区间长度：右区间长度=n。当n为9:1或者99:1时，只要n为常数比例的，算法的时间复杂度总是O(nlgn)。

快排的几种优化方式

对于快速排序，我们有很多优化方式避免快排达到最坏时间复杂度。

1.主元的随机化选取

我们将主元的选取随机化，可以降低快排达到最坏时间复杂度的可能性。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

void quick_sort(int *a, int l, int r)
{
	if (l >= r)
		return;
	int k = rand() % (r - l + 1) + l;  // 产生l到r的随机数
	 // 从a[l]到a[r]中随机选取
	swap(a[l], a[k]);
	int x = a[l];
	int i = l, j = r;
	while (i < j)
	{
		while (a[i] <= x && i<r) ++i;    // 循环结束时a[i]比x大
		while (a[j] >= x && j>l) --j;    // 循环结束时a[j]比x小
		if (i < j)
			swap(a[i], a[j]);       // 交换a[i],a[j]
	}
	// j为分界点
	swap(a[l], a[j]);     // 将主元x放在正确的位置，作为分界点

	// 递归左右子区间
	quick_sort(a, l, j - 1);
	quick_sort(a, j + 1, r);
}

2.三数取中

三数取中比主元的随机化更有优势。
三数取中的意思是：在a[l],a[(l+r)/2],a[r]三个数中选取中间大的数作为主元，可以有效的优化快排效率。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

int Getmid(int *a, int l, int r)
{
	// 取得中间值的下标
}

void quick_sort(int *a, int l, int r)
{
	if (l >= r)
		return;
	swap(a[l], a[Getmid(a, l, r)]);       // 三数取中
	int x = a[l];
	int i = l, j = r;
	while (i < j)
	{
		while (a[i] <= x && i<r) ++i;    // 循环结束时a[i]比x大
		while (a[j] >= x && j>l) --j;    // 循环结束时a[j]比x小
		if (i < j)
			swap(a[i], a[j]);       // 交换a[i],a[j]
	}
	// j为分界点
	swap(a[l], a[j]);     // 将主元x放在正确的位置，作为分界点

	// 递归左右子区间
	quick_sort(a, l, j - 1);
	quick_sort(a, j + 1, r);
}

3.减小递归的栈深度——小区间优化

在C++库函数中sort()的底层实现是有一部分是快排的小区间优化。

我们看一下sort()函数底层实现的源代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14

inline void
    __sort(_RandomAccessIterator __first, _RandomAccessIterator __last,
	   _Compare __comp)
    {
      if (__first != __last)
	{
	// sort函数默认为内省排序，当子数组小于16时返回
	  std::__introsort_loop(__first, __last,
				std::__lg(__last - __first) * 2,
				__comp);
	// 对大致排序过的数组进行插入排序操作
	  std::__final_insertion_sort(__first, __last, __comp);
	}
    }

小区间优化：在子区间的长度小于16时，进行插入排序，减小递归的栈深度。
模拟实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38

void Insert_sort(int *a, int l, int r)
{
	for (int i = l + 1; i < r; ++i)
	{
		if (a[i] < a[i - 1])
		{
			int j = i, k = a[i];
			while (a[i]<a[--j] && j>l);
			int tmp = j;
			while (j < i)
			{
				a[j + 1] = a[j];
				++j;
			}
			a[tmp] = k;
		}
	}
}
void quick_sort(int *a, int l, int r)
{
	if (r - l < 16)           // 在子区间的长度小于16时，进行插入排序，减小递归的栈深度
		Insert_sort(a, l, r);
	int x = a[l];    // 取最左边的值作为主元x
	int i = l, j = r;
	while (i < j)
	{
		while (a[i] <= x && i<r) ++i;    // 循环结束时a[i]比x大
		while (a[j] >= x && j>l) --j;    // 循环结束时a[j]比x小
		if (i < j)
			swap(a[i], a[j]);       // 交换a[i],a[j]
	}
	// j为分界点
	swap(a[l], a[j]);     // 将主元x放在正确的位置，作为分界点

	// 递归左右子区间
	quick_sort(a, l, j - 1);
	quick_sort(a, j+1, r);
}

4.其他优化：

算法导论还提到了其他的优化方法，比如用尾递归减少栈深度，针对相同元素值的快速排序等等。

欢迎大家在下方留言。

大家好，我是希达。

前言

五一期间，我重新搭建了博客，并且更换了简约的博客主题，去掉了背景音乐，增加了在一点程度上吸引读者的二次元人物。

如果大家对此博客网站有何建议，欢迎给我留言。

为什么要搭建博客网站

有很多人想知道：现在有这么多博客网站，比如CSDN，博客园等，为什么还要搭建博客网站呢？

请看一下有代表性的图片：

在CSDN(Chinese Software Developer Network) 上，一篇访问量很高的文章，通常会有刷热度和欢迎回访之类的评论。甚至还有所谓的某领域的专家在不知不觉地带方向(非技术话题)。

我实在是适应不了这种环境，所以搭建自己的博客网站，写出个人学习过程中的心得。
如果我的文章能给你带来一点点思考与启发，我的目的就达到了。

大师的博客

从事计算机行业的的人，一定不要骄傲自大。人外有人，天外有天。以下是与大家分享的大师的博客网站，也是我经常浏览的网站。

1.酷壳（https://www.coolshell.cn/）

陈浩：酷壳
外号：左耳朵耗子。作者编程经验丰富，文笔犀利。

2.陈硕的blog（http://www.cppblog.com/）

博客地址

3.云风的blog

博客地址

4.美团技术团队

博客地址

5.廖雪峰的官方网站

博客地址

文章在精不在多。一篇有深度的文章可以让你驻足许久，提升精神境界。

大家好，我是希达。

前言

今天，在用C语言刷LeetCode时，天真的我发现了leetcode的一个小 ”bug“。

但事实证明：。。。

Welcome to Hexo! This is your very first post. Check documentation for more info. If you get any problems when using Hexo, you can find the answer in troubleshooting or you can ask me on GitHub.

Quick Start

Create a new post

1

$ hexo new "My New Post"

More info: Writing

Run server

1

$ hexo server

More info: Server

Generate static files

1

$ hexo generate

More info: Generating

Deploy to remote sites

1

$ hexo deploy

More info: Deployment